
In Scale Geoffrey West looks at the way that size determines the structure and fate of complex systems (mammals, cities, companies, cells, ...) through Universal Scaling Laws. That is, laws that hold true along the entire scale of the measured quantity. Stated more simply: How does the metabolic rate change, when we increase (scale) the size of a mammal? Linearly? Sublinearly? Superlinearly? What is the relation between the walking speed and the size of a city? (it scales with population size as a power law with β ≈ 1.15)
Scaling laws
This figure shows the log-log plot of Kleiber's law. The basal metabolic rate (in watts) of an animal is roughly proportional to its mass raised to the 3/4 power. Thus, it is also known as the 3/4 scaling law. What is fascinating is the scale of the x-axis: from 0.01 to 10 000 kg. Kleiber's law holds true along seven orders of magnitude.
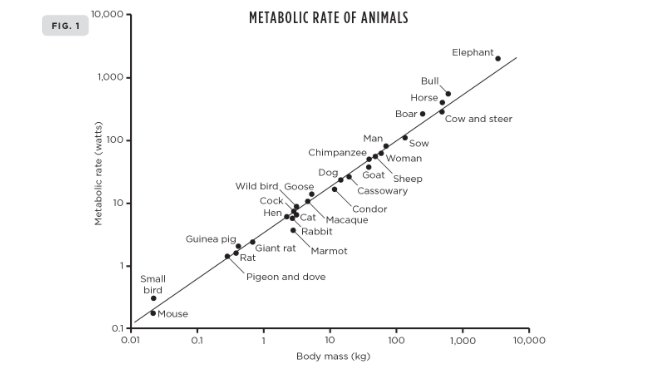
From the book: Metabolic Rate of Animals
This is just one of many scaling laws that West discusses. The general form of scaling laws is this: Y(S) = Y₀ · S^β.
Y denotes the quantity of interest, while S represents size. The constant Y₀ gives the baseline value of Y at unit size. The exponent β determines the scaling behaviour (β equals 3/4 in Kleiber’s law). If β is less than 1, the quantity grows sub‑linearly, lagging behind size; if β is exactly 1, it grows linearly (doubling size doubles Y); and if β is greater than 1, it grows super‑linearly. A negative β means the quantity decreases as size increases.
Godzilla and other things to scale
Why is Godzilla not realistic? Equivalent: Why can we not scale the size of a human by the factor ten? Why should there be a limit to the (possible) size of humans? Answer: Because when you scale up a body, its weight grows faster than its strength. Weight increases with the cube of length, while strength (cross-sectional area) increases only with the square.
Companies and Cities
Companies behave more like organisms than like cities. What does West mean by this? For cities, there are basically two types of scaling laws. For infrastructure, scaling is sublinear: With increased size, we have less streets per person. The scaling exponent here is about 0.85. For socioeconomic outputs, on the other hand, scaling is superlinear: Companies die more quickly, people walk faster, more innovation happens. The scaling exponent here is about 1.15. This is at least partly because interactions between people scale superlinearly with population size. Cities seem "immortal": Even are being nuked to the ground, Hiroshima and Nagasaki recovered and are growing again. Contrast that with companies: Most public traded companies disappear within a few years. As companies grow, they get more unidimensional.
“Cities, on the other hand, become increasingly multidimensional as they grow in size. Indeed, in stark contrast to almost all companies, the diversity of cities, as measured by the number of different kinds of jobs and businesses that comprise their economic landscape, continually and systematically increases in a predictable way with increasing city size. From this perspective it comes as no surprise that the growth and mortality curves of companies closely resemble the corresponding growth and mortality curves of organisms. Both cases exhibit systematic sublinear scaling, economies of scale, bounded growth, and finite life spans. Furthermore, in both cases, the probability of dying, usually referred to as the mortality rate, which is the rate at which deaths are occurring relative to the number still alive, is the same no matter the age of either the animal or the company.”
- Scale, Geoffrey West
Leading Organizations
When West became the president of the Santa Fe Institute, he looked for advice on how to run a successful research institute. He turned to Max Perutz, the crystallographer and Nobel Prize winner who led the Medical Research Council Unit (MRCU) within the Cavendish Laboratory at Cambridge. Under Perutz the MRCU produced nine Nobel Prizes, one of which was the discovery of the DNA structure by Watson and Crick. From Perutz's obituary in the Guardian:
“Impishly, whenever he was asked whether there are simple guidelines along which to organize research so that it would be highly creative, he would say: no politics, no committees, no reports, no referees, no interviews; just gifted, highly motivated people picked by a few men of good judgement.”